Application requirements to design specification: วิธีออกแบบ Design specification สำหรับ Opamp

เมื่อไหร่ก็ตามที่เราต้องออกแบบ Opamp จาก MOS Transistor หรือ BJT เรามักจะเริ่มจาก Design specification เช่น DC open loop gain (AV) หรือ Unity gain bandwidth frequency (UGBW) โดยเราจะใช้ Design specification ดังกล่าวมาคำนวณหาขนาด Width และ Length ของ MOS Transistor ดังเช่นตัวอย่างในบทความนี้ ซึ่งหลายคนอาจสงสัยว่า Design specification เช่น UGBW มาจากไหน

ในบทความนี้ เราจะอธิบายถึงวิธีแปลง Application requirements เพื่อให้ได้ Design specification ที่จะใช้ในการออกแบบ Opamp จาก Transistor โดยเราจะเริ่มจากการอธิบายหลักการของ Negative feedback loop ที่จะใช้เพื่อทำให้วงจรขยายมีความแม่นยำสูงขึ้น และแสดงตัวอย่างการออกแบบ Opamp design specifications

เมื่อไหร่ที่เราต้องใช้ Opamp ?

Opamp ถูกออกแบบมาเพื่อใช้เป็นส่วนหนึ่งของวงจรขยาย โดยใช้หลักการของ Negative Feedback ที่จะช่วยให้เราสามารถออกแบบกำลังขยายที่มีความแม่นยำสูง

ลองพิจารณาหากเรามีสัญญาณ input เข้ามาขนาด 100mV และเราต้องการขยายสัญญาณให้เป็น 1V เราควรทำยังไง ?

หากเราเริ่มต้นด้วยการใช้วงจรขยาย Common Source Amplifier ที่สามารถออกแบบได้ง่ายดายด้วยการใช้ MOS Transistor ไม่กี่ตัว เราก็จะได้วงจรขยายที่มีกำลังขยายถูกกำหนดได้ด้วย

\frac{Vin}{Vout} = -gm \cdot Rout

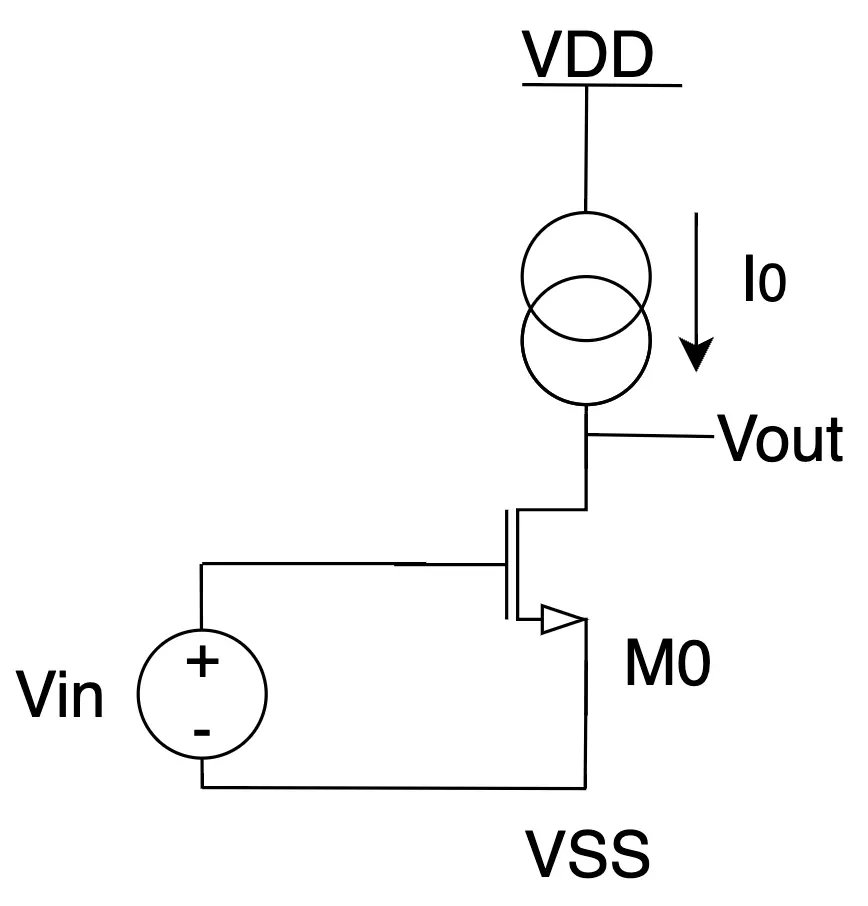
เราจะเห็นว่ากำลังขยายที่เราได้จากวงจร Common Source Amplifier จะขึ้นอยู่กับค่า gm ของ MOS Transistor และค่าความต้านาทาน Rout ที่มาจากความต้านทานขนานของตัวจ่ายประแส (ซึ่งอาจจะออกแบบด้วย PMOS current mirror) ขนานกับความต้านทาน Rds ของ NMOS Transistor M0 ซึ่งทั้งค่า gm และ Rout จะมีการเปลี่ยนแปลงเนื่องจาก process หรืออุณหภูมิ หรือแม้แต่กระแสและแรงดันไบอัสเป็นอย่างมาก หรือเราเรียกกันว่า Process, Temperature and Voltage (PVT) Variation เมื่อเราเปรียบเทียบ Transistor ที่เราออกแบบ แม้จะวางใกล้ๆกัน เราจะเห็นความต่างของ gm ซึ่งอาจสูงถึง 10-20% หากรวมกับตัวแปรอื่นๆแล้วเราอาจจะเห็นความไม่แน่นอนของกำลังขยายที่อาจเปลี่ยนแปลงสูงถึง 50% ดังนั้นการออกแบบวงจรขยายกำลังที่พึ่งพิงค่า gm หรือ Rout จะได้ค่ากำลังขยายที่ไม่มีความแม่นยำเลยแม้แต่น้อย

ใช้หลักการ Negative Feedback เพื่อออกแบบวงจรขยาย

หากเรามีวงจรขยายที่มีกำลังขยายใหญ่มาก ๆ เป็น A เท่า และเรามีวงจรกำลังขยายหรือลดทอน (Attenuation) ที่มีความแม่นยำเป็น B เท่า เราจะได้กำลังขยายจาก Vin ไป Vout เป็น (ลองไปพิสูจณ์สมการกันเองนะครับ)

\frac{Vout}{Vin} = \frac{A}{1+A\cdot B}

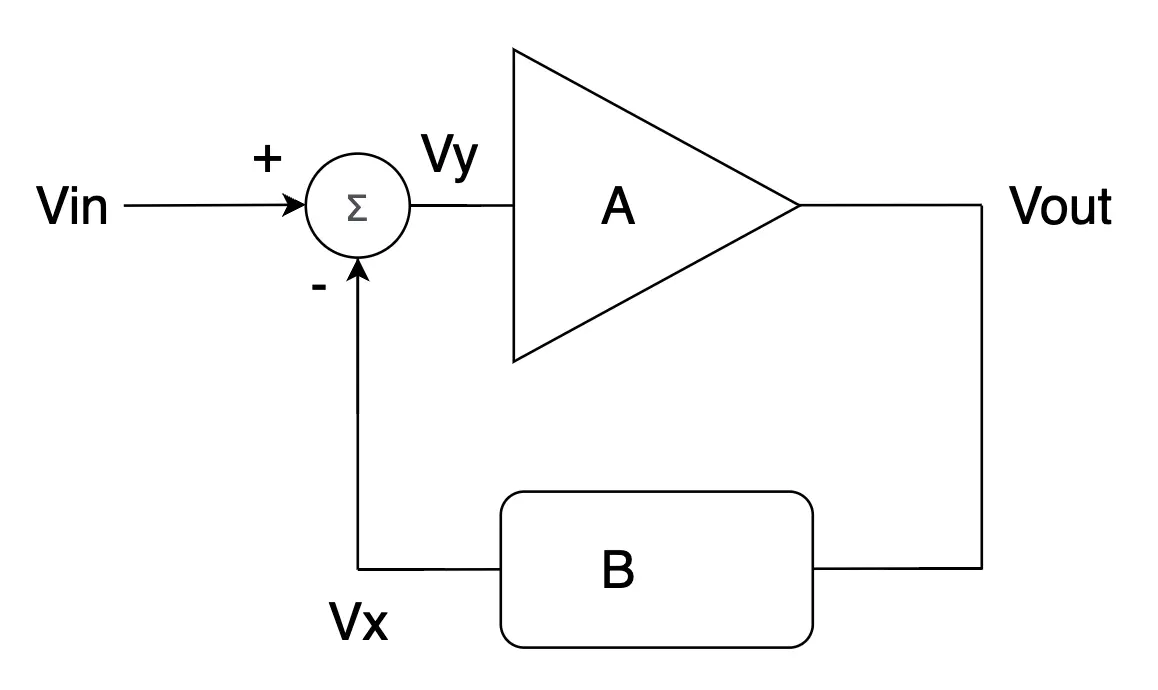
จากสมการ ถ้าหาก A มีค่าใหญ่มากๆ และ A\cdot B \gg 1 เราจะได้ค่ากำลังขยายเป็น

\frac{Vout}{Vin} \approx \frac{1}{B}

ยกตัวอย่างเช่น หากเรามี A = 10,000 เท่า ในขณะที่ B = 1/10 เราจะได้ A / (1+A\cdot B) = 9.99 ซึ่งเราจะได้กำลังขยายที่มีความคลาดเคลื่อนเป็น 0.1\% !!

แล้วหากกำลังขยายที่ได้มีความคลาดเคลื่อนหละ ? เช่น 50\% เราอาจจะได้ A = 5,000 เท่าแทน แต่ B ยังมีความแม่นยำอยู่ที่ 1/10 เราจะได้ A / (1+AB)=5000/(1+5000/10)=9.98 เท่ากับว่าเราได้กำลังขยายที่มีความคลาดเคลื่อนเพียง 0.2% เท่านั้น!!

จะเห็นว่าหากเราออกแบบให้กำลังขยาย A มีค่าสูงมากๆ เราจะได้กำลังขยายวงจรป้อนกลับมีค่าเท่ากับประมาณ B เท่า ซึ่งการออกแบบค่า B ให้มีค่าแม่นยำสามารถทำได้ไม่ยากด้วยการใช้ Resistor divider ดังรูปข้างล่าง ซึ่งจะทำให้เราได้กำลังขยายเป็น

\frac{Vout}{Vin} = \frac{R2}{R1+R2}=\frac{1}{1+\frac{R1}{R2}}

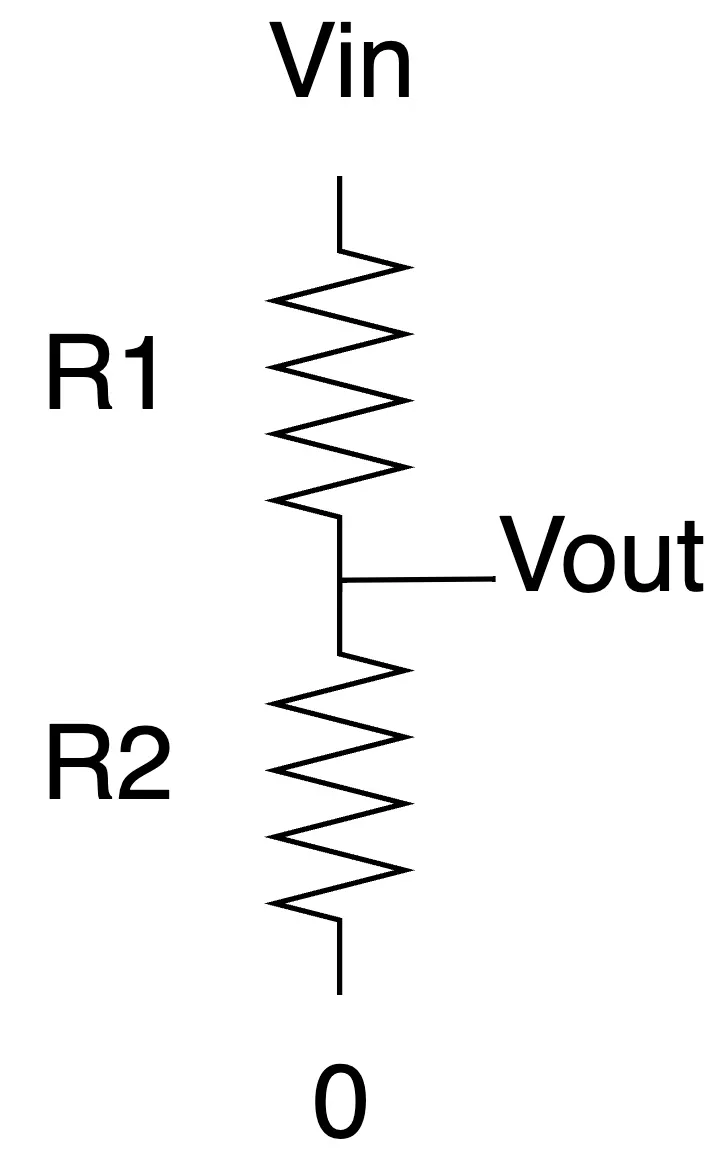
การออกแบบให้กำลังขยายมีค่าแปรผันตามอัตราส่วนของ R จะทำให้เราได้กำลังขยายที่มีความแม่นยำสูง ผสมผสานกับ Layout Technique เราจะได้ความแม่นยำที่สูงกว่า 99% เลย (เราสามารถทำให้ R มีความแม่นยำสูงด้วยการใช้ Layout Technique รวมถึงการเลือกขนาด Width ของ R ที่สูงพอ)

จากข้อสังเกตดังกล่าว เราจะได้สมการความแม่นยำของวงจรขยายแบบ Negative feedback เป็น

error=\frac{1}{B\cdot A} ...(1)

เช่น หากเราต้องการให้ความคลาดเคลื่อน error มีค่าน้อยกว่า 2% โดยที่กำลังขยายอยู่ที่ 10 เท่า เราจะต้องออกแบบให้ A มีค่าเป็น

error=\frac{2}{100} = \frac{1}{\frac{1}{10}\cdot A}

A=500V/V=53.98dB

Negative feedback ที่ความถี่สูง

ในการออกแบบวงจร เรามักจะพิจารณา Bandwidth ของวงจรขยาย โดยวงจรขยายส่วนใหญ่จะมีลักษณะคล้ายกับ Low-pass filter ที่จะมีกำลังขยายสูงที่ความถี่ต่ำ และมีกำลังขยายที่มีขนาดลดลงเมื่อความถี่เริ่มสูงดังรูปที่แสดง Frequency response ของ Opamp ที่จะมีกำลังขยายเป็น 0dB ที่ UGBW และมีอัตราขยายเป็น A_0 ที่ DC

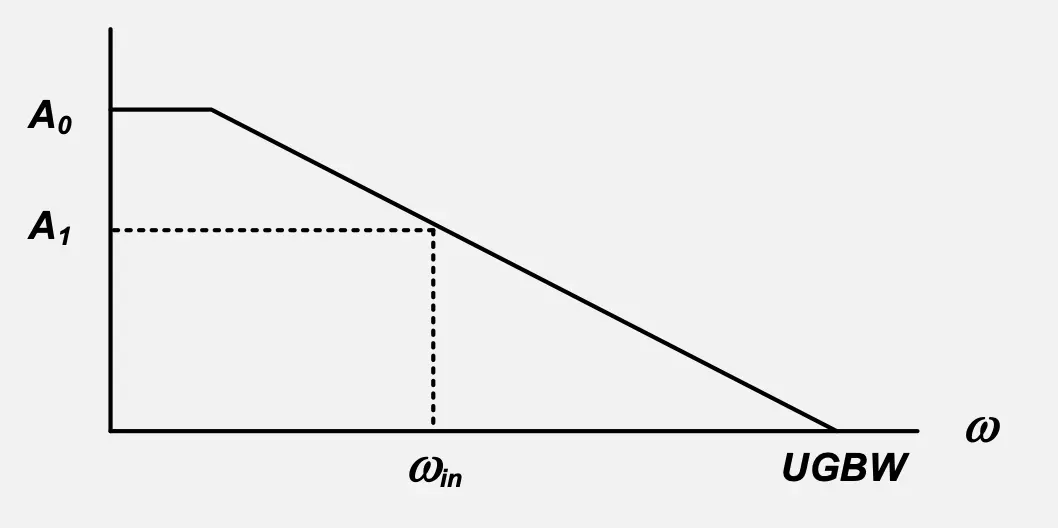
จากสมการก่อนหน้า เรารู้ว่าหากกำลังขยายลดลง ความแม่นยำของกำลังขยายจาก Negative Feedback จะลดลงด้วย เช่น ที่ \omega = 10\cdot UGBW เราจะได้กำลังขยายเป็น A = 20dB ซึ่งจะทำความคลาดเคลื่อน (Error) เพิ่มขึ้นเป็น 10\% !! (สมมติ B = 1)

หากเราพิจารณาว่าวงจรขยายที่เราออกแบบมีลักษณะคล้ายกับ 1st order Low-pass filter (ซึ่งเป็นความจริง หาก Phase margin สูงพอ) เราจะได้ความสัมพันธ์ของ Settling time (\tau) ที่มีค่าขึ้นตรงกับความถี่ cut-off frequency f_c (และความถี่ f_{UGBW}) (อ่านเพิ่มได้ที่นี่) ซึ่ง Settling time จะบอกเราว่าเราต้องใช้เวลาเท่าไหร่ ที่จะทำให้เราได้
Vout = Vin +/- error
ดังรูป

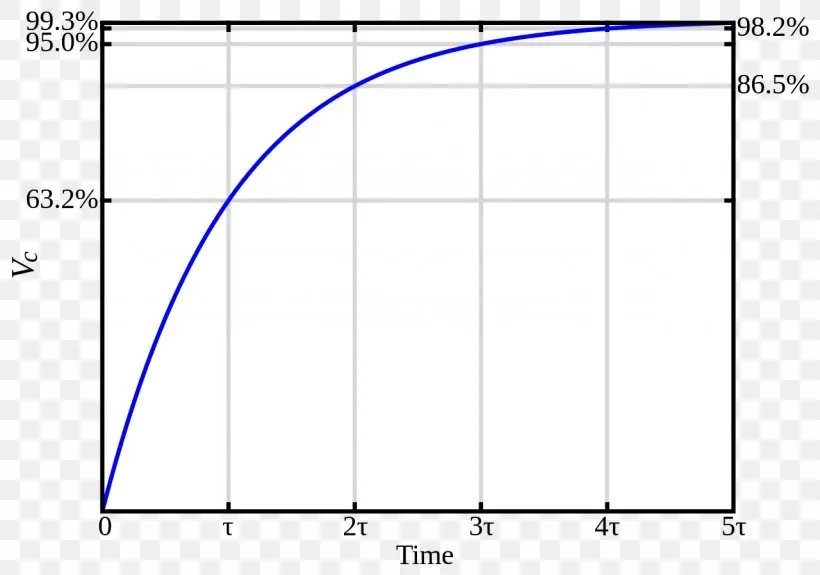
เราจะได้ความสัมพันธ์ระหว่าง Settling time กับ error เป็น

\frac{\tau}{\tau _{UGBW}}=-\frac1 \beta ln(\% error)

UGBW=-\frac1 \beta \frac{ln(\% error)}{\tau}...(2)

โดย \tau คือ Settling time ที่เราต้องการให้ Vout มี error เท่ากับ %error (UGBW ในสมการมีหน่วยเป็น rad/s) ยกตัวอย่างเช่น หากเราต้องการ settling time, \tau = 100ns และ error = 0.1\% และ B (หรือ \beta) = 1/2 เราจะต้องออกแบบให้

UGBW=-\frac{1}{\frac{1}{2}} \frac{ln(0.1/100)}{100 \cdot 10^{-9}}=138.15\cdot 10^6 rad/s=21.99MHz

อย่างไรก็ตาม การทำงานของ Opamp Output ในทางปฏิบัติจะไม่เหมือนกับวงจร RC ซะทีเดียว แต่จะแบ่งเป็นสองช่วงหลักๆ คือช่วงที่ Opamp Output ทำตัวเป็นตัวจ่ายกระแส และอีกช่วงที่เป็นตัวจ่ายแรงดันที่มี Rout ดังกราฟข้างล่าง เราจะเห็นว่าแรงดัน Output voltage จะแบ่งเป็น Slew time (ช่วงที่ Opamp output ทำตัวเป็นตัวจ่ายกระแส) และช่วง Recover time (ช่วงที่ Opamp output ทำตัวเป็นตัวจ่ายแรงดัน) โดยเราจะได้ Settling time เป็น

\tau = \tau_{slew} + \tau_{lin}

โดย \tau_{slew} หรือ Slew time จะเป็นเวลาในช่วงที่ Opamp ทำตัวเป็น current source และ \tau_{lin} หรือ Recovery time จะเป็นช่วงเวลาที่ Opamp ทำตัวเป็นตัวจ่ายแรงดัน

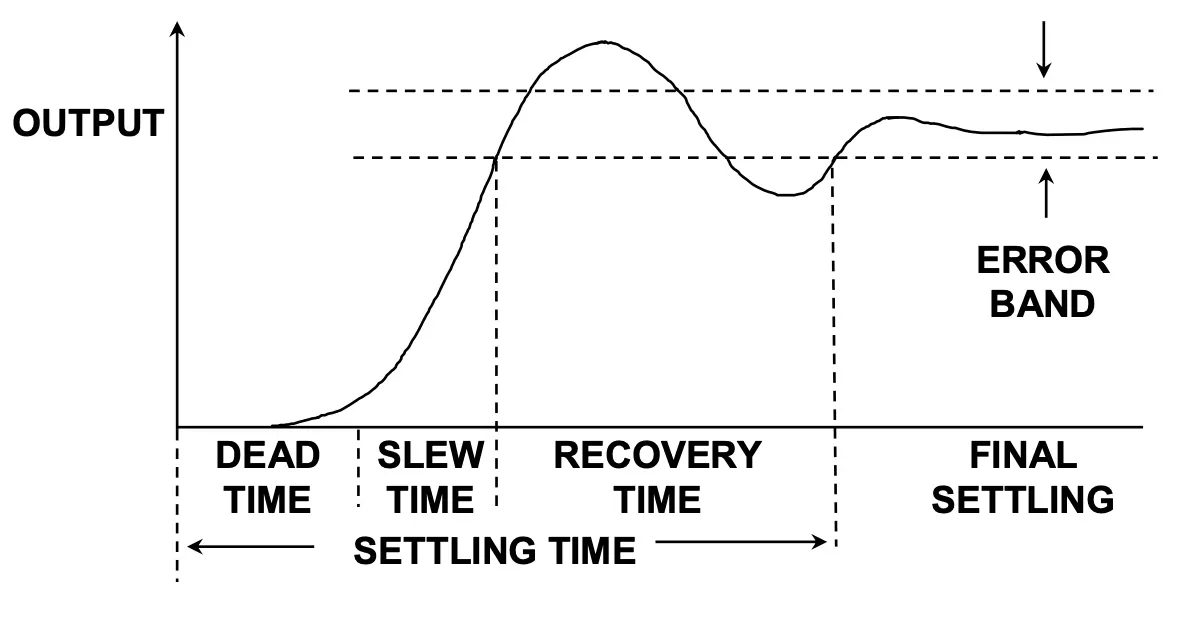
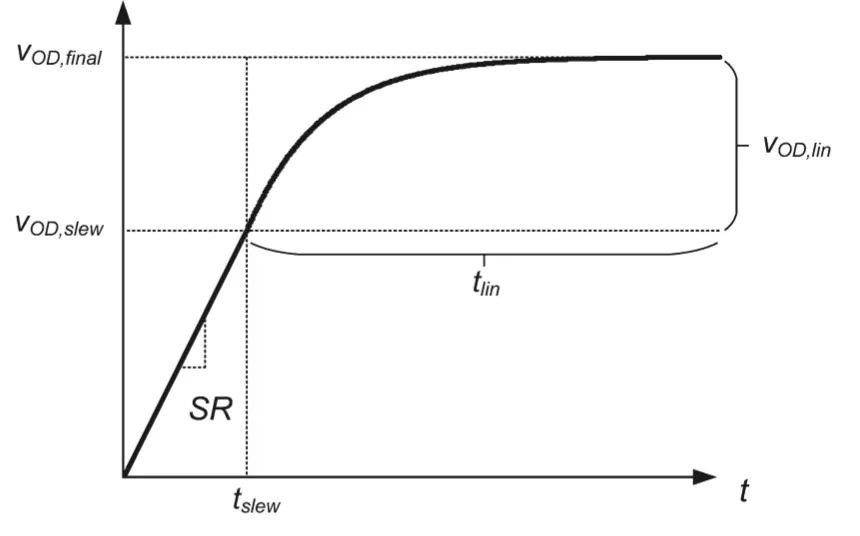
เราสามารถออกแบบค่า \tau_{slew} ได้จากสมการ

\tau_{slew}=V_{slew}/SR

โดย Vslew จะเป็นแรงดันช่วงที่ Opamp ทำตัวเป็นตัวจ่ายกระแส ซึ่งจะคำนวณหาได้ยาก ดังนั้นเราจะประมาณการค่า Voltage ซึ่งจะอยู่ใกล้เคียงกับช่วงของ Voltage ที่เข้าใกล้ Vdsat ของ MOS current mirror ซึ่งจะมีค่าเท่ากับ Output swing ของ Opamp นั่นเอง

ดังนั้นเราจะได้สมการเพื่อหาค่า UGBW จากการรวมผลของ Slew time เป็น

\tau_{lin} = \tau-\tau_{slew}

f_{UGBW}=-\frac1 \beta \frac{ln(\% error)}{2\pi\cdot \left( \tau-\tau_{slew} \right)}...(3)

และเพื่อให้ง่ายต่ำการออกแบบ เราจะกำหนดให้ค่า \tau_{slew} อยู่ที่ประมาณ 30-50% ของ Settling time ทั้งหมด

ยกตัวอย่างเช่น หากเราต้องการ settling time = 100ns และ error = 0.1% และ B (beta) = 1/2 และสมมติให้ Opamp voltage range เป็น 1.4V (เราจะพูดถึงการเลือก Voltage range ภายหลัง) เราจะต้อง ออกแบบให้ (ใช้ตัวอย่างเดียวกับตัวอย่างข้างบน)

\tau_{slew} = 0.3 \cdot \tau = 0.3 \cdot 100ns = 30ns

เราจะได้ Slew rate เป็น

SR=V_{swing}/\tau_{slew}=1.4/30ns=46.67MV/s

และ UGBW เป็น

f_{UGBW}=-\frac1 {(1/2)} \frac{ln(0.1/100)}{2\pi\cdot\left(100ns-30ns\right)}=31.41MHz

วิธีออกแบบ Design Specification ของ Opamp ให้ตรงกับ Application Requirement

เหตุผลหลักที่เราต้องการใช้ Opamp คือการใช้เป็นวงจรขยาย เพื่อขยายด้วยกำลังเท่ากับ 1/B ซึ่งบางครั้งอาจจะเป็น 2 เท่า 10 เท่า หรือแม้แต่ 1 เท่าก็ตาม โดยสิ่งสำคัญที่เราต้องการในวงจรขยายคือ 1) ความแม่นยำ และ 2) เวลาที่ต้องรอให้สัญญาณมีความแม่นยำ (Settling time)

Opamp สำหรับ ADC input

ในงานที่เราต้องการวัดสัญญาณ voltage หรือแม้แต่กระแสที่ไหลผ่าน Resistor เรามักจะต้องการขยายแรงดัน input voltage ให้มีขนาดที่ใหญ่พอเพื่อป้อนเข้าสู่ ADC input ดังรูปข้างล่าง

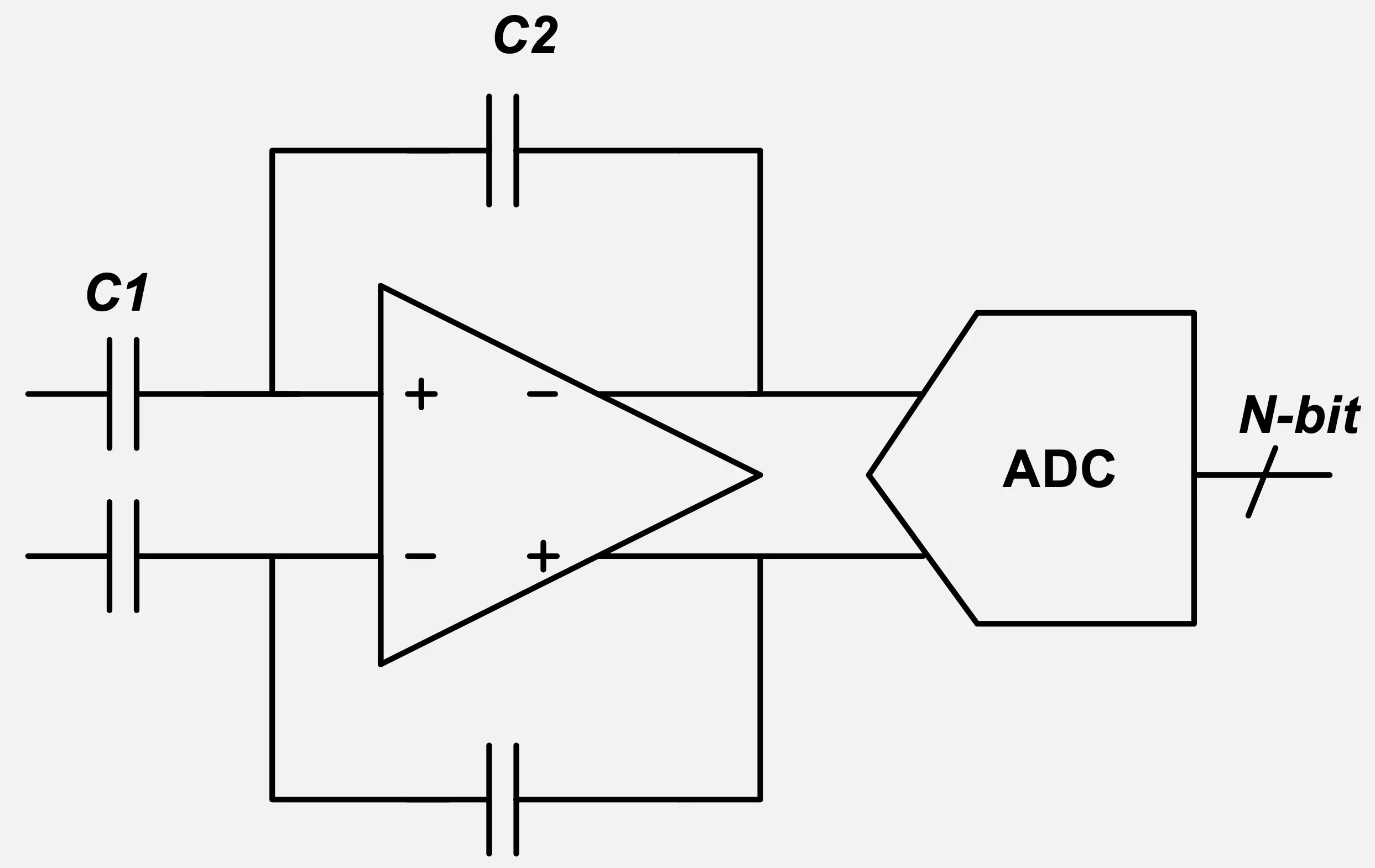
และในการออกแบบ ADC เรามักจะรู้ค่าจำนวน Bit และ Sampling frequency เช่น 9-bit SAR ADC ที่มีความถี่ในการ Sampling เป็น 10MSample/s และสมมติให้ Sampling period เป็นเครื่องหนึ่งของ Sampling frequency period

เราสามารถออกแบบ Opamp Specification โดยเริ่มจากการหา Open Loop Gain จากสมการ (1) โดยเรารู้ว่า Error ของ ADC จะอยู่ที่ LSB/2 เราจะได้

A_{DC}=\frac{1}{\beta\cdot\frac{LSB}{2}}=\frac{1}{\beta\cdot 2^{n+1}}

โดย n คือจำนวนบิทของ ADC จากนั้น เราสามารถหาค่า UGBW จากสมการ (3) เป็น

f_{UGBW}=-\frac{ln\left( \frac{1}{2^{n+1}} \right)}{2\pi\cdot\left(\tau-\tau_{slew}\right)}\cdot\frac{1}{\beta}

ตัวอย่างเช่น จงออกแบบ Opamp Specification สำหรับ 9-bit ADC 10Msample/s เพื่อขยายสัญญาณ input ขนาด 100mV โดย ADC มี Input range อยู่ที่ 0V ถึง 1.8V

จากโจทย์ตัวอย่าง เราต้องออกแบบกำลังขยายเป็น

\frac{1}{b}=\frac{1.8V}{100mV}=18=25.1dB

ดังนั้นเราจะได้ Open loop gain เป็น

A_0=\frac{1}{\beta}\cdot \frac{1}{2^{n+1}}=18,432=85.31dB

จากนั้น เราจะต้องหาค่า Settling time ที่ต้องการจาก ADC Sampling frequency โดยเรารู้ว่า 10MSample/s จะมี period อยู่ที่ 1/10MHz=100ns และโดยทั่วไปแล้ว ADC sampling period จะอยู่ที่ 1/2 ของ period ของ Sampling frequency (ขึ้นอยู่กับ ADC architecture และบางครั้งเราสามารถตั้งใจออกแบบให้ sampling period มีค่ามากกว่า 50% ได้ เพื่อยื่นหยุ่นความต้องการของ Settling time) ดังนั้นเราจะได้ required settling time \tau ≤ 50ns และเราจะเลือก Slew time ให้เป็น 30% ของ Settling time ซึ่งเราจะได้ \tau_{slew}=15ns และ UGBW เป็น

f_{UGBW}=ln\left( \frac{1}{2^{n+1}} \right) \cdot \frac{1}{\beta}\cdot\frac{1}{2\pi\left(\tau-\tau_{slew}\right)}=567.3MHz

นอกจากนี้ เรายังต้องออกแบบให้ Output swing อยู่ระหว่าง 0V ถึง 1.8V อีกด้วย เนื่องจากเราต้องการให้ Opamp output มีค่าเท่ากับ ADC input range ดังนั้นเราจะได้ Slew rate เป็น

SR=V_{slew}/\tau_{slew}=1.8V/15ns=120MV/s

การเลือก Opamp Output swing: ทำไมเราถึงต้องออกแบบ Amplifier output ให้ได้เท่ากับ ADC input ?

หาก ADC ถูกออกแบบให้มี Input range อยู่ที่ 0V ถึง 1V โดยมี resolution อยู่ที่ 9-bit แต่เราสามารถป้อน Output จาก Opamp เข้าสู่ ADC ที่มี Output swing อยู่ที่เพียงระหว่าง 200mV-800mV นั่นเท่ากับว่าจะมีช่วงของ ADC ที่เราไม่ได้ใช้งานเลย นั่นคือ 0-200mV และ 800mV-1V นั่นหมายความว่าเราจะสามารถใช้ ADC ได้เพียงจำนวน voltage step เป็นจำนวน
\frac{\left(800mV-200mV\right)}{\left(1-0\right)}\cdot\frac{1}{2^{9+1}}= 307
ขั้นจากทั้งหมด 512 ขั้น (voltage steps) นั่นหมายความว่า Effective number of bit (หรือ ENOB) ของ ADC จะเหลือเพียงประมาณ 8.2 bit แทนที่จะเป็น 9 bit นั่นเอง

ดังนั้น เราควรคำนึงถึง Output swing ของ Opamp โดยต้องออกแบบให้ Opamp มี Output swing เท่ากับ Input range ของ ADC

Opamp สำหรับงานอื่น ๆ

สำหรับการออกแบบวงจร Opamp เพื่อใช้ในงานอื่น ๆ เช่นการใช้เป็น Voltage follower หรือการออกแบบ Opamp ในวงจร LDO Regulator เราจะใช้หลักการเดียวกับวิธีคำนวณหา Design Specification ของ Opamp สำหรับ ADC input ที่เราได้แสดงก่อนหน้า โดยเราต้องคำนึงถึงความแม่นยำของสัญญาณ Output ที่เราได้หลังจากการขยายสัญญาณ และความเร็วในการ Settle สัญญาณ

สรุป

ในบทความนี้เราได้พูดถึงหลักการใช้ Negative feedback เพื่อทำให้วงจรขยายมีความแม่นยำสูงขึ้น และวิธีการออกแบบ Opamp design specifications โดยเริ่มจาก Application requirements รวมถึงแสดงตัวอย่างการออกแบบ Design spec ของ Opamp เพื่อใช้สำหรับ ADC input